Tenstorrent Wormhole Series Part 7: Bits of the MatMul
Previously, in part 6, I took a deep dive into Tensix Vector, but if you're buying Tenstorrent hardware, you almost certainly want fast matrix multiplication. Furthermore, if that is your view, then everything else on the chip is secondary to matrix multiplication: SRAM and DRAM are for storing matrices close to the compute logic, Tensix Vector is for operating on matrix multiplication results without having to send them back to the host over PCIe, and so on.
Back in part 5, we saw one representation of a T tile, emphasizing the RISC-V cores. A different representation of the same thing instead emphasizes Tensix Matrix and the data paths to/from it:
The above diagram requires a few remarks:
- Part 5's diagram shows Tensix instruction pipes and Tensix Sync between the "T" RV cores and the Tensix execution resources; those things do exist, but I've elided them from today's diagram.
- Any of the various Tensix execution resources can be instructed from any of the "T0" / "T1" / "T2" RV cores, but today's diagram shows the traditional setup whereby "T0" instructs Tensix Unpack, "T1" instructs Tensix Matrix and Tensix Vector, and "T2" instructs Tensix Pack.
- Similarly, any RV core can issue read or write commands to either of the NoC routers, but today's diagram shows the simplest possible convention of a 1:1 relationship between RV cores and NoC routers (the recently merged tt-metal#13376 enables more complex relationships).
- The thin arrows in and out of the NoC routers are the various tile-to-tile connections we saw all the way back in part 1.
The focus might be on Tensix Matrix, but the data path between Tensix Matrix and L1 goes through Tensix Unpack and Tensix Pack. The very quick summary of these units is that they can perform some light data type conversion and some light reshaping, but mainly just shovel data between L1 and SrcB / SrcA / Dst. The bidirectional arrow on the diagram between Tensix Pack and L1 is there because Tensix Pack can perform either L1 = Dst or L1 += Dst, with the latter eliminating some of the need for Tensix Unpack to write to Dst. Tensix Pack can also perform some flavors of ReLU, though only as L1 = ReLU(Dst) or L1 += ReLU(Dst), and not as L1 = ReLU(L1 + Dst).
The sub-32-bit types that Tensix Unpack can write to SrcA and SrcB include:
With that interlude complete, we can finally look at Tensix Matrix. It is capable of a few different operations, but the big one is matrix multiplication, doing Dst += SrcB @ SrcA, where Dst and SrcB are both 8x16 and SrcA is 16x16:
The TT-Metal API tends to expose 32x32 blocks, matmul for which can be built out of the 8x16 matmul, one possible arrangement being:
For the primitive 8x16 operation, what gets applied to each scalar element of Dst is d = d + a0·b0 + a1·b1 + ⋯ + a15·b15, where ai ranges over a column of SrcA and bi ranges over a row of SrcB. For a 32x32 block, the primitive 8x16 operation needs to be applied 16 times in total (because there are 8 chunks of Dst, and each chunk requires a 32-element dot product rather than just a 16-element dot product).
The scalar + and · in the previous paragraph are floating-point addition and multiplication. If you're not a hardware designer, you might view floating-point addition and multiplication as magical primitive operations provided by hardware. If you are a hardware designer, you'll know that nothing is magic: floating-point addition and multiplication need to eventually be implemented via a mixture of integer comparisons, shifts, additions, and multiplications. To really reinforce the point that nothing is magic, I can show you code for bf16 fused-multiply-add implemented using just integer operations. Any actual hardware would be described in (System)Verilog rather than C, but there are more people who can read C than Verilog. If you look through that code, you'll see a few major pieces:
- Decompose the bf16 inputs to their sign / exponent / mantissa (lines 20-21).
- For normal numbers, re-attach the implicit one bit at the top of the mantissa (line 21). For denormal numbers, use
__builtin_clzand<<to find and reposition their most significant one bit (lines 22-24). - Check for any input being NaN or infinity, and return an appropriate NaN or infinity if so (lines 33-45).
- Perform the multiply: xor of signs, integer addition of exponents, integer multiplication of mantissas (lines 31, 47-49).
- Perform the addition: determine the largest exponent, use
>>on the mantissa of the other value to equalize the exponents, then integer add or subtract the mantissas (lines 51-73). - Turn the result back into bf16:
__builtin_clzand<<or>>to get exactly 10 bits of mantissa, clamp exponent to the range 0-255 (possibly another>>here if the value is denormal), then pack sign and exponent and mantissa into 16 bits (lines 75-85). - Considering all the bits thrown away by
>>in previous steps, perform rounding on the result (rounding to nearest, ties to even). This is just line 88, though it relies heavily onp_m <<= 3, z_m <<= 3and onsticky_shiftin earlier steps.
If you're aiming for full IEEE754 conformance, then all of the above steps are required. If instead you're designing hardware for AI, then any step that can be removed and/or simplified is a massive win: each Tensix Matrix unit on a Wormhole chip wants to perform 2048 floating-point multiplies and 2048 floating-point additions per cycle, and there are 80 Tensix Matrix units on each chip, so any cost savings in either multiplication or addition get amplified 16,3840 times. Even a small simplification becomes noticable when amplified that much. I don't know exactly what simplifications Tenstorrent have opted for, but there are potential savings in every step:
- Perform decomposition somewhere else (e.g. in Tensix Unpack rather than Tensix Matrix).
- Treat all denormals as zero, thus saving on
__builtin_clzand<<. - Correctly handle only some cases of inputs being NaN or infinity.
- Use only some of the mantissa for multiplication rather than all of it.
- If adding more than two values together, determine the largest exponent of all of them, then use
>>to equalize all their exponents at once (some academic work calls this a Class IV multi-term adder). All the mantissas can then be added together using a multiple-input integer adder, rather than a tree of two-input adders. - If the result is going to immediately feed into step 1 of another multiply/add, skip step 6 and the subsequent step 1. Additionally, if the result is denormal, treat it as zero to save on
>>. - Use a cheaper rounding mode: either rounding toward zero (no rounding bits required), or rounding to nearest with ties away from zero (just one rounding bit required).
Treating denormals as zero on input (step 2) and on output (step 6) are relatively common simplifications; usually even CPUs have options for it. The more unusual simplifications are in steps 4 and 5. For step 4, if you want to be able to multiply a variety of floating-point formats between bfp2 and tf32, then you'd normally need an 11b by 11b multiplier for this step:
That said, fp8 (e5m2) only requires 3b by 3b multiply, and bf16 only requires 8b by 8b, so the full 11b by 11b might feel wasteful if lower-precision operations the majority of your workload. The particular simplification that Tenstorrent have opted for in Wormhole is a 7b by 5b multiplier, which can be invoked up to four times to cover (almost) the full range:
This has a number of interesting implications:
- All of bfp2 / bfp4 / fp8 (e5m2) can get away with just LoFi(delity).
- Bfp8 requires LoFi + HiFi2 to fully consume all the mantissa bits, but you could opt for just LoFi if throwing away two bits from
SrcAis acceptable. - Bf16 requires all of LoFi + HiFi2 + HiFi3 + HiFi4 to consume all the mantissa bits, but only a few bits are consumed by HiFi4, so it could reasonably be skipped, and not very much is consumed by HiFi3, so it too could possibly be skipped.
- Fp16 requires all of LoFi + HiFi2 + HiFi3 + HiFi4, and even then, one bit from
SrcAisn't consumed. - If more than just LoFi is used, there's an extra rounding step (to the precision of
Dst) between each fidelity stage. - The programmer chooses how many fidelity stages their workload requires.
At this point, we can cross-check with the advertised TFLOP/s numbers. We'd expect 4.096 TFLOP/s from each Tensix Matrix unit when LoFi is in use (e.g. for fp8), half that when LoFi + HiFi2 is in use (e.g. for bfp8), and half that again when all of LoFi + HiFi2 + HiFi3 + HiFi4 are required (e.g. for fp16). With 72 usable Tensix Matrix units on an n150s board and 128 usable on an n300s board, this would mean:
| n150s | n300s | |
|---|---|---|
| Just LoFi, e.g. fp8 (e5m2) | 294.9 TFLOP/s | 524.3 TFLOP/s |
| LoFi+HiFi2, e.g. bfp8 | 147.5 TFLOP/s | 262.1 TFLOP/s |
| LoFi+HiFi2+HiFi3+HiFi4, e.g. fp16 | 73.7 TFLOP/s | 131.1 TFLOP/s |
Meanwhile, the one-pager from the Tenstorrent sales page reports:
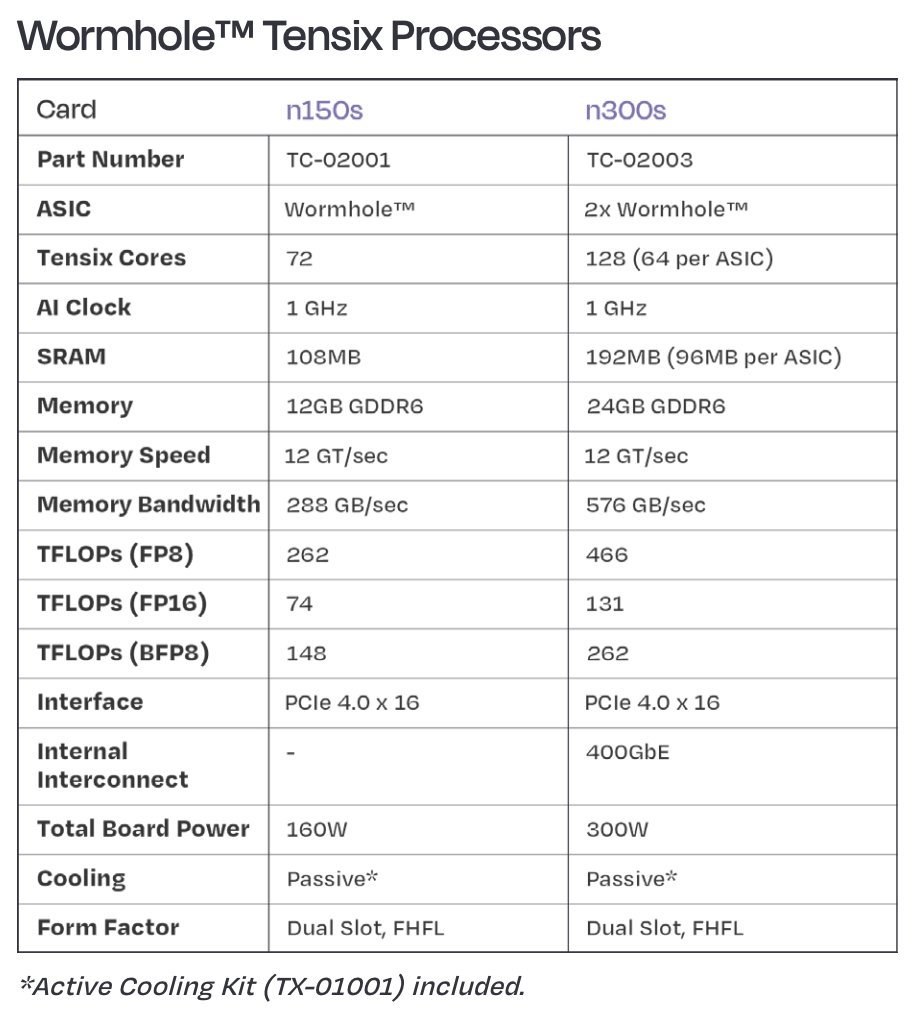
The bfp8 and fp16 numbers are exactly as expected. The oddity is the fp8 number, which is only 88.9% (i.e. sixteen eighteenths) of expected. This suggests that at such low precision, the bottleneck becomes data transfer (e.g. 16 cycles to multiply a 32x32 tile, but 18 cycles to get the data in or get the data out).
To hit these TFLOP/s numbers, "all" you have to do is write code for one of the RV "T" cores to issue a matrix multiplication instruction every cycle, and write code for the other four RV cores to keep data flowing in and out at the right rate. The Macro-Op Expander and Replay Expander seen in part 5 help with this task: the expanders can output a Tensix instruction every cycle without themselves needing to be instructed every cycle, giving the RV cores a bit of time to do other things (such as control flow). Then repeat this 72 times for an n150s board, or 128 times for an n300s board. In either case, that'll result in several hundred RV cores busily working away!
That wraps up part 7; there will likely be a long gap before the next part due to a certain factory game expansion pack being released next week.





